Unit Converter ▲
Unit Converter ▼
| From: | To: |
Surface Area of a Cylinder
A cylinder is a common three-dimensional geometric shape that consists of two identical circular bases and a lateral surface connecting these bases. The cylinder has wide applications in mathematics, engineering, and science. Understanding the calculation of its surface area is crucial for solving various practical problems. This article will explain the surface area of a cylinder in detail, including its formula and how to apply it.
1. Definition of a Cylinder
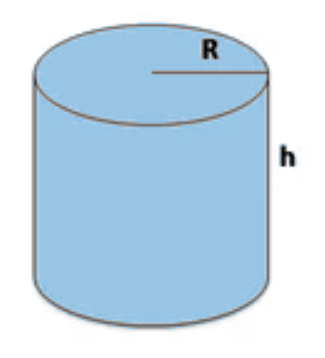
Before discussing the surface area, let's first define the cylinder. A cylinder consists of two parallel circular bases and a lateral surface that connects these two bases. The key parameters of a cylinder are:
- Radius (\(r\)): The radius of the circular base of the cylinder.
- Height (\(h\)): The vertical distance between the two bases of the cylinder.
The shape of a cylinder is simple, but its surface area calculation involves multiple parts. We need to calculate the areas of the two bases and the lateral surface.
2. Surface Area Calculation for a Cylinder
The surface area of a cylinder consists of three parts:
- Base Area: A cylinder has two identical circular bases, so the total base area is \(2 \pi r^2\).
- Lateral Surface Area: The lateral surface can be "unfolded" into a rectangle. The width of the rectangle is the circumference of the base, \(2 \pi r\), and the height of the rectangle is the height of the cylinder, \(h\). So, the lateral surface area is \(2 \pi r h\).
The total surface area of a cylinder is the sum of the areas of the two bases and the lateral surface. Therefore, the surface area formula for a cylinder is:
\(S = 2 \pi r^2 + 2 \pi r h\)
Where:
- \(2 \pi r^2\) is the area of the two circular bases.
- \(2 \pi r h\) is the lateral surface area.
3. Explanation of the Surface Area Formula
Let's break down the surface area formula further:
- Base Area: The base of the cylinder is a circle, and its area is calculated using \( \pi r^2 \). Since there are two identical bases, the total base area is \(2 \pi r^2\).
- Lateral Surface Area: The lateral surface of the cylinder can be unfolded into a rectangle. The width of the rectangle is the circumference of the base (\(2 \pi r\)) and the height is the cylinder’s height (\(h\)). Therefore, the lateral surface area is \(2 \pi r h\).
By adding the areas of the two bases and the lateral surface, we obtain the total surface area of the cylinder:
\(S = 2 \pi r^2 + 2 \pi r h\)
4. Applications of Cylinder Surface Area
The surface area of a cylinder has numerous applications in various fields. For example:
- Container Design: In designing cylindrical containers like water tanks or oil barrels, the surface area is crucial to calculate the amount of material needed to construct the container.
- Heat Exchanger Design: Some heat exchangers or pipes are cylindrical. The surface area is important for understanding the heat transfer efficiency and surface treatment requirements.
- Packaging Design: In the production of cylindrical packaging, such as cans or bottles, the surface area helps determine the amount of label, coating, or packaging material required.
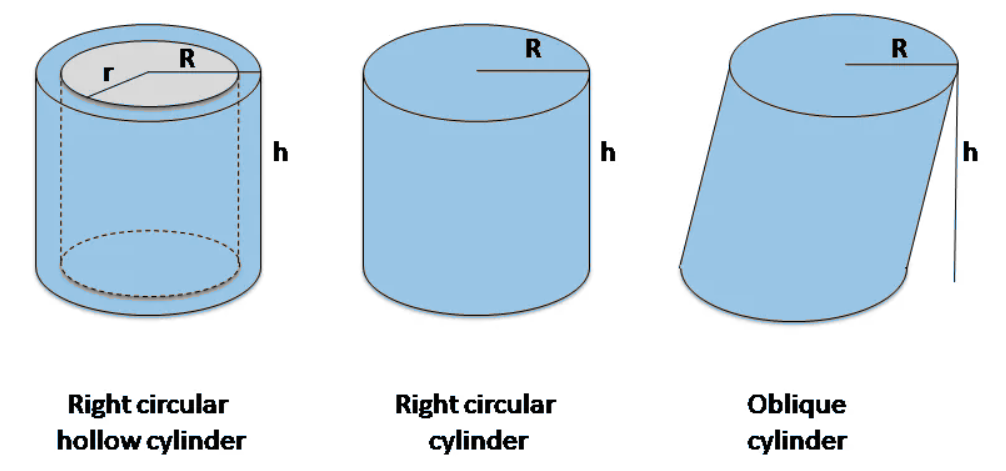
5. Variants of Cylinders and Their Surface Area
In addition to the standard cylinder, there are several variants with slightly different surface area formulas:
- Half Cylinder: A half-cylinder is simply half of a cylinder, typically formed by cutting the cylinder in half along its height. Its surface area includes half of the base, half of the lateral surface, and the cutting plane's area.
- Hollow Cylinder: A hollow cylinder has two different radii: an outer radius (\(R\)) and an inner radius (\(r\)). The surface area includes the areas of the two circular rings and the two lateral surfaces.
- Half Hollow Cylinder: A half hollow cylinder is half of a hollow cylinder. Its surface area involves the areas of the two half-ring bases and half of the lateral surface.
The surface area formulas for these variants differ depending on their specific geometric characteristics, but the basic principles remain the same.
Surface Area Formulas for Cylinders and Hollow
The surface area formula for a cylinder is:
\(S = 2\pi r^2 + 2\pi r h\)
Where: \( r \) is the radius of the base, \( h \) is the height of the cylinder.
2. Surface Area Formula for a Half Cylinder
The surface area formula for a half cylinder is:
\(S = \pi r^2 + \pi r h + r h\)
Where: The first term \( \pi r^2 \) represents the area of the half-circle base, The second term \( \pi r h \) is half of the lateral surface area, The third term \( r h \) is the area of the cutting plane.
3. Surface Area Formula for a Hollow Cylinder
The surface area formula for a hollow cylinder is:
\(S = 2\pi (R^2 - r^2) + 2\pi (R + r) h\)
Where: \( R \) is the outer radius, \( r \) is the inner radius, \( h \) is the height of the hollow cylinder.
4. Surface Area Formula for a Half Hollow Cylinder
The surface area formula for a half hollow cylinder is:
\(S = \pi (R^2 - r^2) + \pi (R + r) h + 2(R - r) h\)
Where: The first term \( \pi (R^2 - r^2) \) represents the area of the two half-ring bases, The second term \( \pi (R + r) h \) is half of the lateral surface area, The third term \( (R - r) h \) is the area of the cutting plane.
What is the lateral surface area of a cylinder?
The Curved or lateral Surface Area of a Cylinder is given by 2 × π × r × h where, r = base radius, and h = height of the cylinder.
 Home
Home Back
Back